Ângulo entre os ponteiros do Relógio – parte 3

(Reprodução de parte do livro Matemática em Detalhes. Proibida a reprodução total ou parcial)

Já estudamos nas partes 1 e 2 como calcular o ângulo entre os ponteiros de um relógio.

Neste texto aplicaremos o que vimos para resolver uma questão que caiu na prova do ITA de 2011.

(ITA-2011) Entre duas superposições consecutivas dos ponteiros das horas e dos minutos de um relógio, o ponteiro dos minutos varre um ângulo cuja medida, em radianos, é igual a

$$ (A)\ \frac{23}{11} \pi \ \ \ \ \ \ (B)\ \frac{13}{6} \pi \ \ \ \ \ \ (C)\ \frac{24}{11} \pi \ \ \ \ \ \ (D)\ \frac{25}{11} \pi \ \ \ \ \ \ (E)\ \frac{7}{3} \pi \ \ \ \ \ \ $$

Resolução:

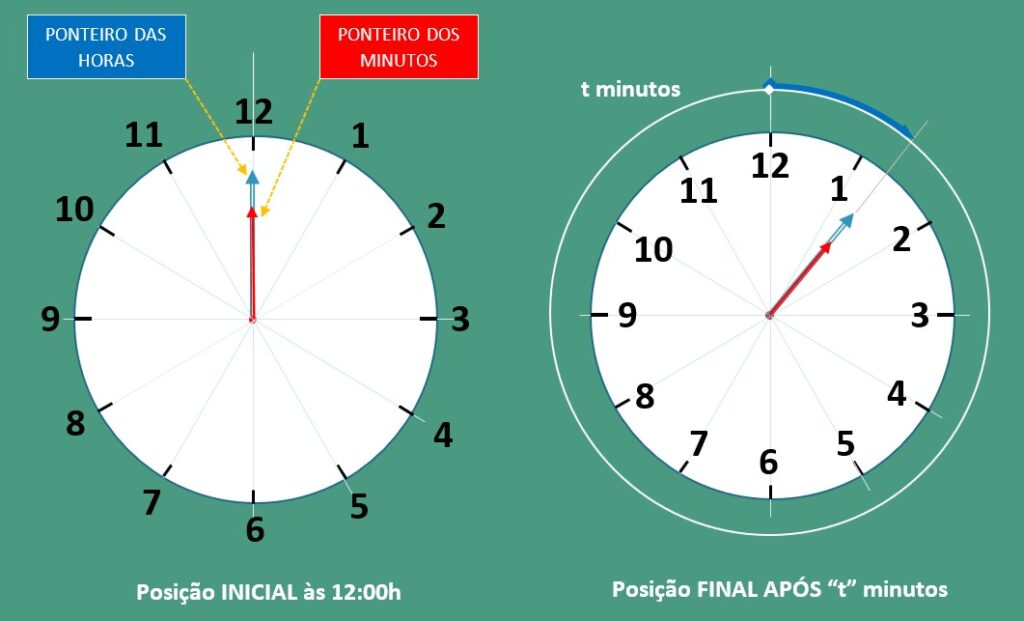
Primeiramente é de se notar que uma das superposições dos ponteiros das horas e dos minutos ocorre exatamente às 12:00h.

A partir de então, há outras onze superposições dos ponteiros: a primeira pouco após, mas não exatamente às 1:05h, a seguinte pouco após às 2:10h e assim até novamente chegarmos às 12:00h (vide figura [01] abaixo.

Outro fato notável é que o intervalo de tempo entre duas superposições consecutivas dos ponteiros das horas e dos minutos é exatamente o mesmo para qualquer par (de horários) de superposições consecutivas que escolhermos.

Isto é, o tempo que decorre entre a superposição que ocorre às 12:00h até a superposição seguinte que ocorre um pouco após 1:05h é exatamente o mesmo tempo que leva entre a superposição que ocorre, por exemplo, pouco após às 4:20h e aquela que ocorre após às 5:25h.

Uma forma de ver isso mais facilmente é imaginar um relógio cujo fundo que contém os números possa girar independente dos ponteiros.

Imagine a superposição que ocorre pouco após à 4:20h e o movimento dos ponteiros para que haja a superposição seguinte que deve ocorrer após às 5:25h, conforme figura [02] abaixo.

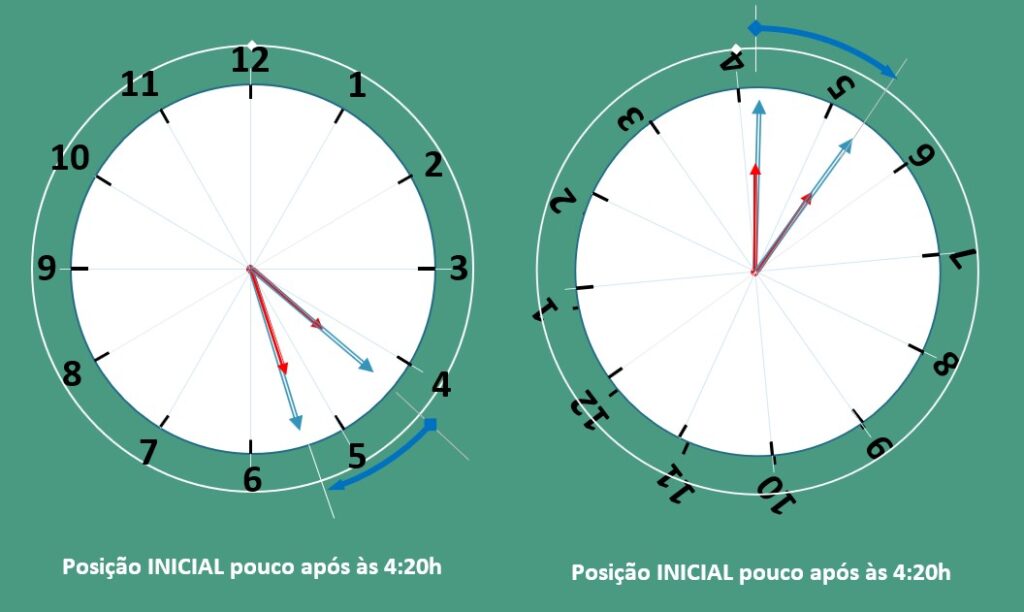
Se girarmos o fundo do relógio que contém os números até que a posição do número 12 coincida com os ponteiros das horas e dos minutos no momento em que estão superpostos pouco após às 4:20h evidentemente teríamos exatamente o mesmo problema se partíssemos da posição original do fundo às 12:00h.

Na figura {02} acima o desenho do relógio à direita foi “girado” de tal modo que os ponteiros se encontram nas mesmas posições da figura [01] anterior.

Feita essa explicação preliminar, podemos voltar ao nosso problema.

Conforme já observamos inicialmente, escolheremos a posição inicial (primeira superposição) como sendo às 12:00h (vide figura [01]).

A vantagem dessa escolha é evidente uma vez que, neste caso, conhecemos exatamente a hora indicada pelos ponteiros: 12:00h.

Seja x o deslocamento em radianos do ponteiro dos minutos para ir da primeira superposição (12:00h) para a superposição seguinte (pouco após às 1:05h).

Repare que para o ponteiro sair da primeira superposição (12:00h) até alcançar novamente o ponteiro das horas, ele deverá dar uma volta inteira no relógio antes de sobrepor-se novamente ao ponteiro das horas, isto é, seu deslocamento será maior do que 360°.

Seja t o tempo transcorrido entre a primeira e a segunda superposição.

Sabemos dos posts anteriores que o ponteiro dos minutos se desloca 30° a cada 5 minutos.

Lembremos que

$$ 180°= \pi \ radianos $$ e, portanto, $$ 30°= \frac{\pi}{6} \ radianos $$

Assim podemos estabelecer para o ponteiro dos minutos que:

$$ \frac{\pi}{6} \ radianos \to 5 \ minutos $$ $$ x \ radianos \to t \ minutos $$

Daqui concluímos que o tempo transcorrido entre duas superposições consecutivas é dado por:

$$ t= \frac{30}{\pi}x \ \ minutos \ … \ (1) $$

Também dos tópicos que estudamos anteriormente, sabemos que o ponteiro das horas se desloca 30° a cada 60 minutos.

Antes de prosseguir observe que enquanto o ponteiro dos minutos se deslocou de um ângulo x o ponteiro das horas se deslocou

$$ (x-2\pi) $$

Isso porque o ponteiro dos minutos “anda mais depressa” e na superposição seguinte já deu uma volta completa no relógio indo da posição em que está o número 12 até a posição do novo “encontro” (superposição) com o ponteiro das horas que por sua vez se deslocou apenas da posição onde está o número 12 até o novo encontro que ocorrerá após às 1:05h.

Assim podemos estabelecer para o ponteiro das horas que:

$$ (x-2\pi) \to t $$ $$ \frac{\pi}{6} \to \ 60 \ \min $$

Daqui concluímos que o tempo transcorrido entre duas superposições consecutivas é dado por::

$$ t= \frac{360}{\pi}(x-2 \pi) \ … \ (2) $$

De (1) e (2) concluímos que:

$$ \frac{30}{\pi}x= \frac{360}{\pi}(x-2 \pi) $$

Resolvendo a equação acima obtemos que:

$$ x= \frac{24}{11} \pi \ rad $$

Como se vê é uma questão muito simples para quem já estudou os movimentos do ponteiro do relógio. Caso ainda não tenha visto as aulas em vídeo, nas quais fizemos o estudo dos movimentos dos ponteiros do relógio, clique AQUI para ver a parte-1 ou AQUI caso esteja interessado na parte-2.

Então até o próximo artigo e não se esqueçam: foco, dedicação e trabalho!