Ângulo entre os ponteiros de um relógio – parte 2
(Reprodução de parte do livro Matemática em Detalhes. Proibida a reprodução total ou parcial)
Introdução
Vimos anteriormente, na parte 1, como calcular o ângulo entre os ponteiros das horas e dos minutos.
Para tanto foi necessário definirmos previamente o relógio ideal.
Para quem não viu ainda esta parte 1 clique aqui.
Pois bem, no artigo de hoje daremos continuidade à aula do artigo anterior, mostrando como calcular o ângulo entre os ponteiros dos segundos e das horas e também entre os ponteiros dos segundos e dos minutos.
Na parte 1 já estudamos o movimento do ponteiro das horas, isto é, aquele que indica a hora e nesta parte 2, estudaremos o movimento dos ponteiros dos minutos e dos segundos.
Movimento do ponteiro dos MINUTOS em função do tempo
Na parte 1 fizemos uma simplificação ao estudar o movimento do ponteiro das horas: desprezamos o ponteiro dos segundos.
Na prática, simplesmente consideramos apenas os horários em que a fração que indica os segundos era nula, isto é, consideramos apenas os horários em que o ponteiro dos segundos estava exatamente sobre o número 12 do relógio.
Por exemplo: 3h:40min; 11h:35min; 8h:17min.
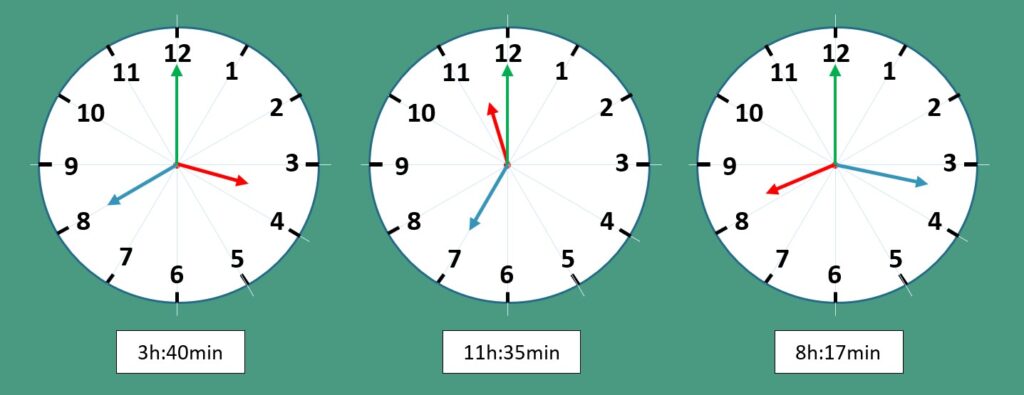
Nestes três exemplos anteriores os tempos indicados não fazem qualquer menção à fração indicativa dos segundos, isto é, os tempos “param” na unidade minutos (3h:40min; 11h:35min e 8h:17min) o que nos faz supor que o ponteiro dos segundos está exatamente sobre o número 12 do relógio, conforme pode ser visto na figura [01] na qual o ponteiro dos segundos está na cor verde.
Vamos agora, nesta parte 2, estudar o deslocamento do ponteiro dos minutos.
Para tanto considere o deslocamento do ponteiro dos minutos das 3h:00min às 3h:05min, conforme figura [02] abaixo.
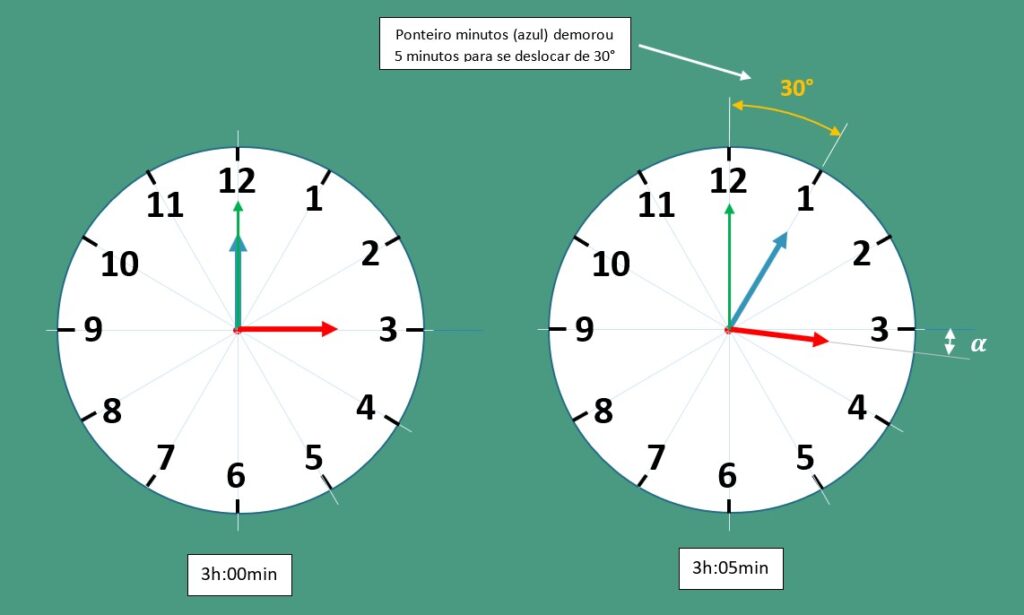
Pela figura fica claro que, das 3h:00min às 3h:05min, o ponteiro dos minutos (na cor azul) se desloca de um ângulo de 30º e leva exatamente 5 minutos para fazê-lo, o que é equivalente a afirmar que a cada 1 minuto (60 segundos) o ponteiro dos minutos se desloca o equivalente a 6°, ou ainda, que a cada 10 segundos desloca-se 1°.
Apenas um parênteses aqui: não confunda as unidades minutos e segundos indicativas de tempo daquelas indicativas de ângulo (deslocamento – submúltiplos da unidade de medida de ângulo “grau”).
O contexto em que são empregados permitem a distinção de quando estamos nos referindo à unidade de tempo e quando estamos nos referindo à unidade de ângulo (deslocamento).
Então, atenção na leitura!
Temos aqui a chave para o estudo do deslocamento do ponteiro dos minutos em função do tempo: para se deslocar de 1°, o ponteiro dos minutos leva 10 segundos.
Então, podemos calcular os ângulos ente quaisquer dois dos ponteiros do relógio: horas e minutos; horas e segundos e minutos e segundos.
Tomemos como exemplo o problema que pede para calcular o ângulo entre os ponteiros do relógios às 3h: 05min: 40 seg.
A figura [03] a seguir ilustra o nosso problema.
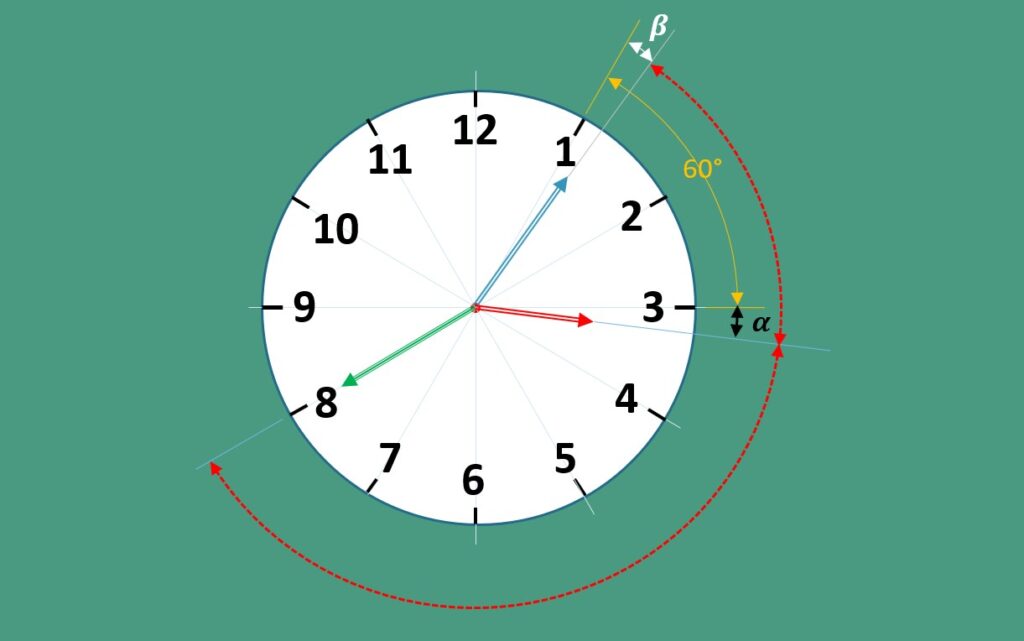
Note que o ponteiro das horas não está exatamente sobre o número 3, já que não são exatamente 3h.
O ponteiro dos minutos também não está exatamente sobre o número 5, já que não exatamente 3h: 5min.
Por outro lado, às 3h: 05 min: 40 seg, o ponteiro dos segundos está exatamente sobre o número 8 (observe 3h: 05 min: 40 seg).
Outra observação importante é a de que das 3h até às 3h: 05 min: 40 seg, passaram-se 5 minutos e 40 segundos, ou seja, 340 segundos (lembre-se de que 5 minutos = 5 X 60 seg = 300 seg, logo 5 minutos e 40 segundos = 300 + 40 = 340 segundos).
Nesses 340 segundos o ponteiro das horas deslocou-se de um ângulo alfa e o ponteiro dos minutos deslocou-se de um ângulo beta, conforme mostra a figura [03] anterior.
Estes dois ângulos podem facilmente serem calculados com o vimos na parte 1 e nesta parte 2.
Com efeito, para o ponteiro das horas teremos:
$$ \alpha \to \ 40 \ segundos \ $$ $$ \ 30° \to \ 60 \ min \ = \ 3600 \ segundos \ $$Logo:
$$ \alpha \ =\ 30°\ .\frac{\ 40}{\ 3600}\ =\frac{\ 1}{\ 3°}\ =\frac{\ 1}{\ 3}\ .60’\ =\ 20’\ $$Observe que no cálculo acima usamos o fato de que o ângulo de medida 1° é igual ao ângulo de medida 60′ (sessenta minutos).
Desse modo, podemos encontrar o ângulo entre os ponteiros das horas (em vermelho) e dos segundos (em verde) às 3h: 05 min: 40 s, que seria dado por (vide figura [03]):
$$ 150°\ -\alpha \ = 150°\ -\ 20′ \ = \ 149° 40’\ $$
`Da mesma forma podemos calcular qual o deslocamento do ponteiro dos minutos (em azul) no intervalo entre 3h: 05 min e 3h: 05 min: 40 seg, ou seja, qual foi o deslocamento em 40 segundos.
Representando pela letra grega “beta” este deslocamento (vide figura [03]) e lembrando do que estudamos até aqui desde a parte 1, temos que:
$$ \beta \to \ 40 \ segundos \ $$ $$ \ 1°\to \ 10 \ segundos \ $$ $$ \beta \ =\ 4°\ $$Com isso é possível calcular o ângulo entre os ponteiros das horas e dos minutos que é dado por (vide figura [03]):
$$ \ 60°\ +\alpha \ -\beta \ =\ 60°\ +\ 20’\ -\ 4°\ =\ 56°\ 20’\ $$Evidentemente também podemos encontrar o ângulo entre os ponteiros dos minutos (em azul) e dos segundos (em verde) às 3h: 05 min: 40 s, que seria dado por (vide figura [03]):
$$ \ 210°\ -\beta \ =\ 210°\ -\ 4°\ =\ 206°\ $$Conclusão
Esta parte 2 finaliza o estudo que foi iniciado na parte 1, isto é, após os estudos dessas duas partes é possível resolver uma variedade grande de exercícios relacionados a este tema.
Por exemplo: você saberia dizer em quais horas (exatamente), no intervalo das 3h às 4h os ponteiros das horas e dos minutos formam um ângulo reto?
Em uma outra lado abordaremos este problema, ok?
Fiquem ligados!
Até a próxima!

Seja o primeiro a comentar!